We prefer todays money to that of tomorrow due to our pressing needs for consumption and cost of abstinence form the present consumption, fall in the value of money tomorrow due to inflation and possible use of money when exchanged for tomorrows money.
Thus, when we lend money, we forego all the advantages of liquidity, ready usability, safety etc. we abstain from present consumption when lent to somebody or invested. All these will lead to what is called the time preference for money. To compensate for that, future money will have to be discounted to the present time.
Tomorrows money or money a year hence has to be discounted to the present day by discount rate suitable as a reward for the above sacrifices. This is called discounting, used for cash flows or dividends to be received in future and to be calculated for the present.
Similarly an investment of today, if it is to be returned after a year or so, todays money has to be compounded by a discount rate to equate to the future funds likely to be available in return. This is called compounding. Compounding and discounting are thus tow major methods of analyzing the time value of money.
Time preference rate: the time preference for money is generally expressed by an internal rate. It is a risk free rate.
Required Rate of Return = Risk free rate + Risk premium
The risk free rate compensates for time while risk premium compensates for Risk.
Read Also :
Compound value and compound interest: investments involve more than one period. The interest that is paid on the principal as well as on any interest earned but not withdrawn during the earlier periods is called compound interest. The process of finding the future value of a payment or series of payments when applying the concept of compound interest is known as compounding.
Compound value of a lump sum:
Future sum = principal + interest
A finance manager is required to make decisions on investment, financing and dividend in view of the company's objectives.
The decisions as purchase of assets or procurement of funds i.e. the investment/financing decisions affect the cash flow in different time periods. Cash outflows would be at one point of time and inflow at some other point of time, hence, they are not comparable due to the change in rupee value of money. They can be made comparable by introducing the interest factor.
In the theory of finance, the interest factor is one of the crucial and exclusive concept, known as the time value of money.
Time value of money means that worth of a rupee received today is different from the same received in future. The preference for money now as compared to future is known as time preference of money. The concept is applicable to both individuals and business houses.
Reasons of time preference of money :
1) Risk :
There is uncertainty about the receipt of money in future.
2) Preference for present consumption :
Most of the persons and companies have a preference for present consumption may be due to urgency of need.
3) Investment opportunities :
Most of the persons and companies have preference for present money because of availabilities of opportunities of investment for earning additional cash flows.
Importance of time value of money :
The concept of time value of money helps in arriving at the comparable value of the different rupee amount arising at different points of time into equivalent values of a particular point of time, present or future.
The cash flows arising at different points of time can be made comparable by using any one of the following :
- by compounding the present money to a future date i.e. by finding out the value of present money.
- by discounting the future money to present date i.e. by finding out the present value(PV) of future money.
1) Techniques of compounding :
i) Future value (FV) of a single cash flow :
The future value of a single cash flow is defined as :
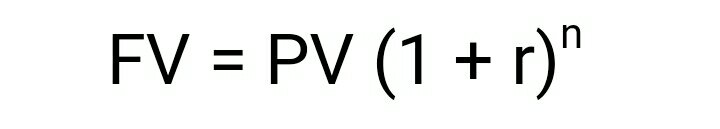
Where, FV = future value
PV = Present value
r = rate of interest per annum
n = number of years for which compounding is done.
If, any variable i.e. PV, r, n varies, then FV also varies. It is very tedious to calculate the value of (1 + r)^n, so different combinations are published in the form of tables.
These may be referred for computation, otherwise one should use the knowledge of logarithms.
ii) Future value of an annuity :
An annuity is a series of periodic cash flows, payments or receipts, of equal amount. The premium payments of a life insurance policy, for instance are an annuity.
In general terms the future value of an annuity is given as :
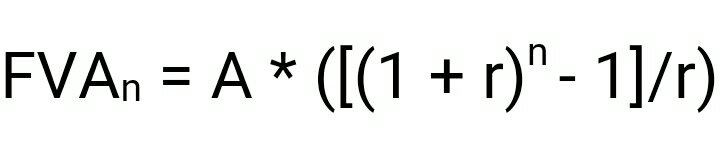
Where,
FVAn = Future value of an annuity which has duration of n years.
A = Constant periodic flow
r = Interest rate per period
n = Duration of the annuity
Thus, future value of an annuity is dependent on 3 variables, they being, the annual amount, rate of interest and the time period, if any of these variable changes it will change the future value of the annuity.
A published table is available for various combination of the rate of interest 'r' and the time period 'n'.
2) Techniques of discounting :
i) Present value of a single cash flow :
The present value of a single cash flow is given as :
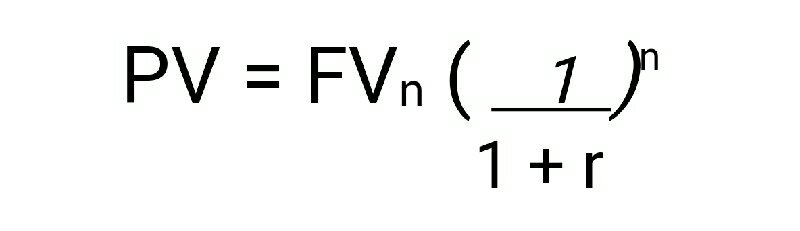
Where,
FVn = Future value n years hence
r = rate of interest per annum
n = number of years for which discounting is done.
From above, it is clear that present value of a future money depends upon 3 variables i.e. FV, the rate of interest and time period. The published tables for various combinations of
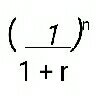 are available.
are available.ii) Present value of an annuity :
Sometimes instead of a single cash flow, cash flows of same amount is received for a number of years. The present value of an annuity may be expressed as below :
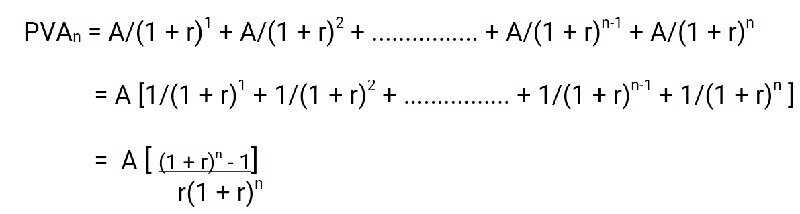
Where,
PVAn = Present value of annuity which has duration of n years
A = Constant periodic flow
r = Discount rate.










0 comments:
Post a Comment